仲間たちと一緒に江陵へ行った。
仲間の一人がKTXでサクッと行けば、ランチタイムに出発してディナータイムには戻ってこれるって言ったんだ。毎日、灰色の壁に囲まれてモニターばかり見ているから、それくらいなら久しぶりにパッと行ってくるのもいいかなって思った。ネットで調べたら清涼里駅から出発して江陵まで約1時間半くらいかかるらしい。そういえば去年済州島に行って以来、海を一度も見ていない。もちろん毎年海を見る必要はないけどね…
いつもより少し余裕のある日、私たちはかばんをそのまま肩にかけて江陵へ向かった。到着するまで何しようかと考えているうちに、もう列車は楊平を過ぎている。
昔は江陵に行くには高速バスで5時間もかかった。子供の頃から車酔いがひどかった私は、大関嶺を越えるのが本当に辛かった。くねくねと終わりのない大関嶺は、いつも稼働中の遠心分離器のように私の精神を体から引き離してしまい、その宇宙遊泳はいつも大関嶺の端にある下堤民願を通り過ぎるまで続いた。でも2015年末、平昌郡珍富面と江陵市城山面を貫通する全長22キロの大関嶺トンネルが完成し、それ以降はバスで5時間以上かかっていたソウル-江陵の走行時間が約1時間半に短縮されたんだ。(ハレルヤ) おかげで江陵とソウルは日帰り生活圏内に入り、平昌オリンピックも成功裏に開催できたってわけ。
とにかくそのおかげで車酔いの心配もなく、快適に江陵に到着して有名なチョダンスンドゥブを食べて、すぐに安木海辺のカフェ街に向かった。安木海辺の次の目的地は申師任堂の生家である烏竹軒だったけど、一度海を見た私たちは日差しの良い海辺近くのカフェの屋上に居座ってしまった。そういえばソウルで落星台を何度も通り過ぎても姜邯賛将軍の生家を訪れたことはない。「何でもその場にちゃんとあればいいのさ。」と言っていると、誰かが海を見ながら一言を投げかけた。
同僚 A: ここからあの水平線までの距離はどれくらいかな?
同僚 B: さあ?10キロ?100キロ?
気になるなら計算すればいいんだ。
— 私が計算してあげるよ。
私はいつもペンと手帳を持ち歩いているから、そんなの朝飯前だ。
— まず、私たちが4階建ての建物の屋上にいて、座って海の方を見ているわけだ。建物の1階を3mと仮定すると、私たちが海を見る目線の高さは地面から約13mだ。
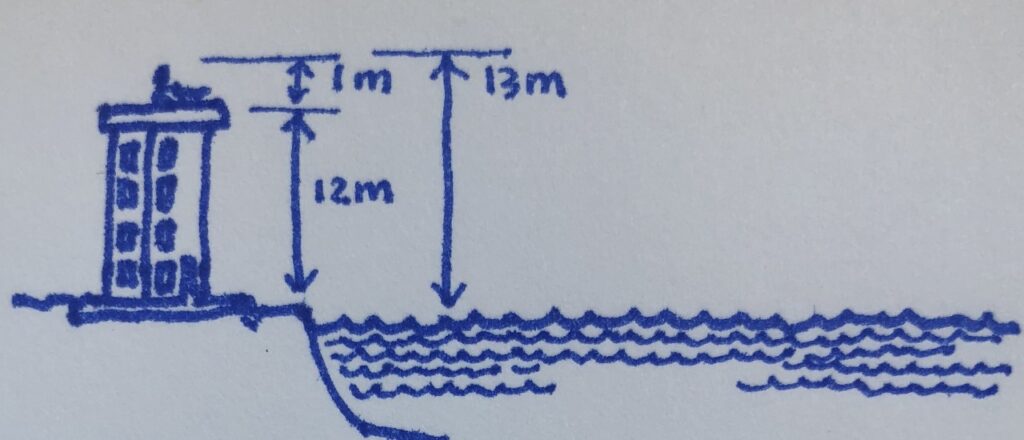
— そして、私たちの視線が水面と接する部分まで直線で表現すると、地球の中心から直角三角形を描けるよね。こんなふうに。
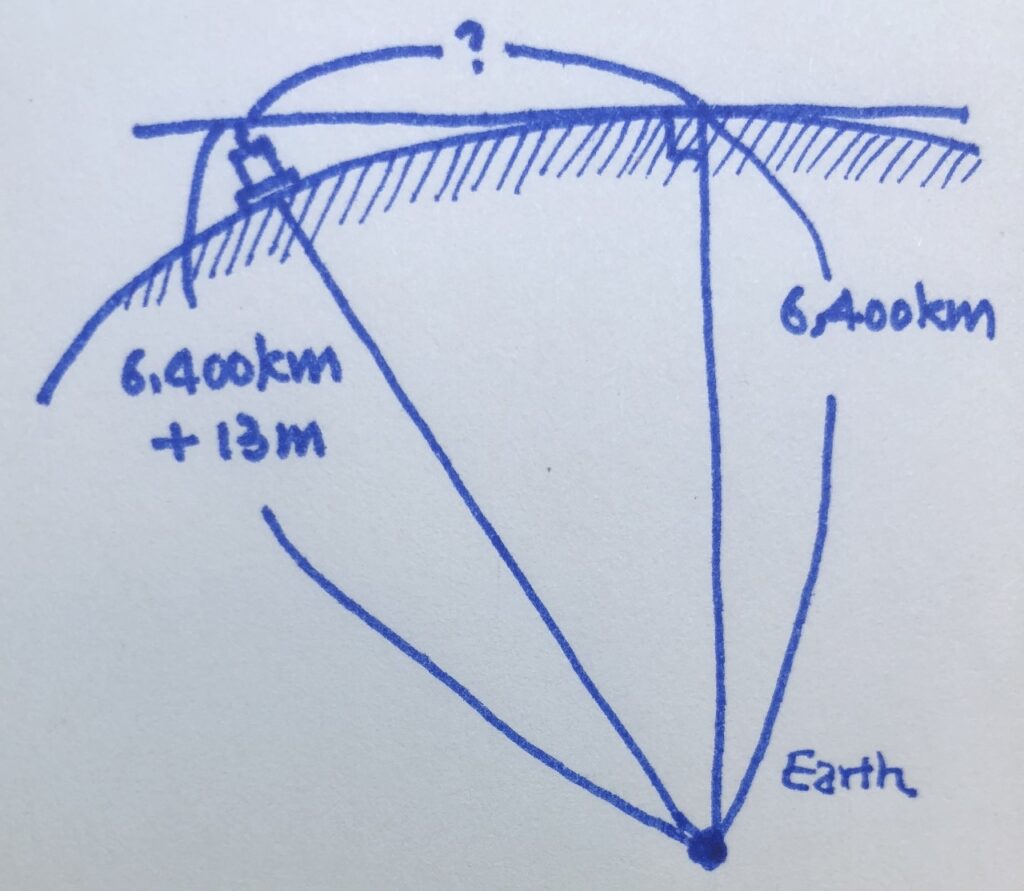
— さて、私たちが求めたい距離をxとして、計算を簡単にするために地球の半径をyとしよう。ここにピタゴラスの定理を適用すれば、一番長い辺である(地球の半径+13m)の2乗は、他の2辺である地球の半径、yの2乗と求めたい距離、xの2乗を足した値と等しくなるんだよね。さあ、展開して地球の半径である6,400kmをyに代入して計算するだけだよ。

式を展開して不要な変数を消去して解を求めていると、突然人々が『ちょっとタバコを吸ってくるね。計算続けてて。』と言った。その間にスマートフォンの工学用計算機を使ってすぐに距離を求められたんだけど、その距離は13キロくらいで、自転車を走らせれば1時間くらいで十分に到達できる距離だった。少し待つと人々が階段を上ってくる足音が聞こえた。
— 距離求めたよ。距離はね。
同僚 B: あ、でも烏竹軒行かなくてもいいかな?
同僚 A: ここまで来たら烏竹軒くらいは行ってみないとね…。
同僚 B: じゃあ、早く動こう!
— …
(ソウルの姜邯賛将軍の生家にも一度も行かない人が烏竹軒に何しに行くんだよ!それよりそんなに気になってた距離を求めたんだから。さっき100キロじゃないかって言ってたよね?実際の距離とのギャップを知ったらかなり驚くはずだよ。)
同僚 B: ところで、申師任堂の名前って、任堂なの?師任堂なの?
同僚 A: 師任堂だよ。
同僚 B: それって本名?仮名?
(そこで仮名はないでしょ。師任は号だよ。名前はちゃんとした文献には出てない。そして、距離は13キロだってば?)
しかし、人々は師任堂がニックネームでも、コードネームでも、あるいは彼女が紳士であっても全く気にしないという表情でゆっくりと建物を降りていった。